Programming with Python

Analyzing Data from Multiple Files

Learning Objectives

• Use a library function to get a list of filenames that match a simple wildcard pattern.
• Use a for loop to process multiple files.

We now have almost everything we need to process all our data files. The only thing that’s missing is a library with a rather unpleasant name:

import glob

The glob library contains a single function, also called glob, that finds files whose names match a pattern. We provide those patterns as strings: the character * matches zero or more characters, while ? matches any one character. We can use this to get the names of all the HTML files in the current directory:

print(glob.glob('*.html'))

['01-numpy.html', '02-loop.html', '03-lists.html', '04-files.html', '05-cond.html', '06-func.html', '07-errors.html', '08-defensive.html', '09-debugging.html', '10-cmdline.html', 'index.html', 'LICENSE.html', 'instructors.html', 'README.html', 'discussion.html', 'reference.html']

As these examples show, glob.glob’s result is a list of strings, which means we can loop over it to do something with each filename in turn. In our case, the “something” we want to do is generate a set of plots for each file in our inflammation dataset. Let’s test it by analyzing the first three files in the list:

import numpy
import matplotlib.pyplot

filenames = glob.glob('*.csv')
filenames = filenames[0:3]
for f in filenames:
    print(f)

    data = numpy.loadtxt(fname=f, delimiter=',')

    fig = matplotlib.pyplot.figure(figsize=(10.0, 3.0))

    axes1 = fig.add_subplot(1, 3, 1)
    axes2 = fig.add_subplot(1, 3, 2)
    axes3 = fig.add_subplot(1, 3, 3)

    axes1.set_ylabel('average')
    axes1.plot(data.mean(axis=0))

    axes2.set_ylabel('max')
    axes2.plot(data.max(axis=0))

    axes3.set_ylabel('min')
    axes3.plot(data.min(axis=0))

    fig.tight_layout()
    matplotlib.pyplot.show(fig)

inflammation-01.csv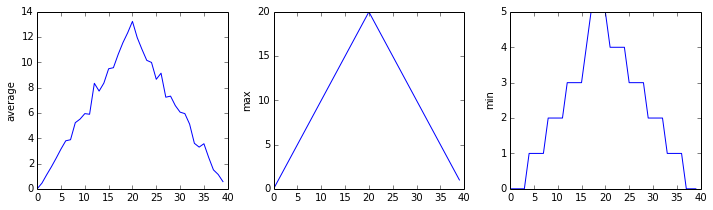

inflammation-02.csv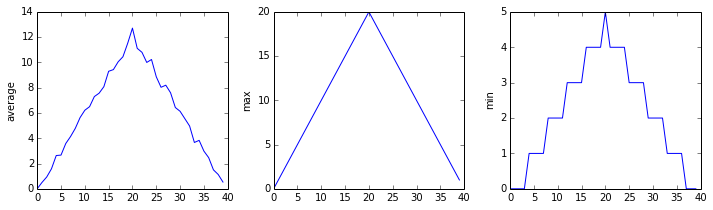

inflammation-03.csv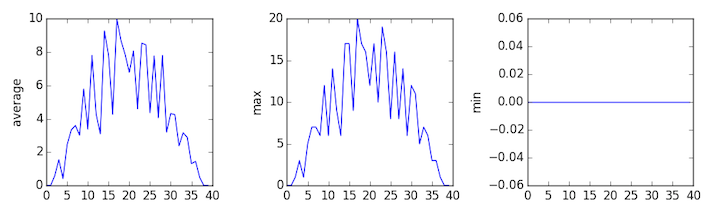

Sure enough, the maxima of the first two data sets show exactly the same ramp as the first, and their minima show the same staircase structure; a different situation has been revealed in the third dataset, where the maxima are a bit less regular, but the minima are consistently zero.