# grafica usando la función grafica_onda a un tiempo tt
tt = 10
fig, ax, ax_x, ax_y = haz_ejes()
grafica_onda(X[:,:,tt], Y[:,:,tt],a[:,:,tt], tt, ax, ax_x, ax_y)
plt.show()
Facultad de Ciencias DFG 2024-1
En este notebook repasaremos algunos conceptos básicos de cinemática de ondas. Puedes descargar el notebook de la página de Classroom del curso y modificarlo a tu gusto.
Referencia principal: Cushman-Roisin y Beckers (2011), Apéndice B
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.animation import FuncAnimation
from IPython import display
plt.ioff()
<matplotlib.pyplot._IoffContext at 0x7f869d545520>
def grafica_onda(x, y, a, tt, ax, ax_x, ax_y, A=2):
# quitar marcas en los ejes
ax_x.tick_params(axis="x", labelbottom=False)
ax_y.tick_params(axis="y", labelleft=False)
# longitud de matrices dirección x y y
s = np.shape(x)
nx = s[1]
ny = s[0]
# gráfica 2D de "a"
pc = ax.pcolormesh(x, y, a, cmap=cm.coolwarm, vmin=-A, vmax=A)
# grafica "a" a lo largo de x y y
ax_x.plot(x[int(nx/2),:],a[int(nx/2),:], color='navy')
ax_y.plot(a[:,int(ny/2)],y[:,int(ny/2)], color='navy')
# Agrega líneas en cero
ax_x.axhline(0, color='0.5')
ax_y.axvline(0, color='0.5')
# grafica líneas en x y y a lo largo de ls cuales graficamos "a"
ax.axvline(x[0,int(nx/2)], color='navy')
ax.axhline(y[int(ny/2),0], color='navy')
# Límites de los ejes
ax.set_xlim(np.min(x),np.max(x))
ax.set_ylim(np.min(y),np.max(y))
ax_x.set_ylim(-A,A)
ax_y.set_xlim(-A,A)
# Etiquetas de los ejes
ax.set_xlabel('x')
ax.set_ylabel('y')
ax_x.set_ylabel('a')
ax_y.set_xlabel('a')
# Agrega una etiqueta con la marca del tiempo correspondiente
ax_y.text(0.5, 1.2,'t=%d s' %tt, transform=ax_y.transAxes)
def haz_ejes(figsize=(6,6)):
# Definiciones para los ejes
left, width = 0.1, 0.65
bottom, height = 0.1, 0.65
spacing = 0.03
rect_pcolor = [left, bottom, width, height]
rect_x = [left, bottom + height + spacing, width, 0.2]
rect_y = [left + width + spacing, bottom, 0.2, height]
# start with a square Figure
fig = plt.figure(figsize=figsize)
ax = fig.add_axes(rect_pcolor)
ax_x = fig.add_axes(rect_x, sharex=ax)
ax_y = fig.add_axes(rect_y, sharey=ax)
return(fig, ax, ax_x, ax_y)
# Animación en el tiempo
def animate(tt):
ax_x2.clear()
ax_y2.clear()
grafica_onda(X[:,:,tt], Y[:,:,tt],a[:,:,tt], tt, ax2, ax_x2, ax_y2, A=Amax)
Por simplicidad (de presentación y para graficar) consideremos una onda plana en dos dimensiones, es decir, una señal física que ocupa el plano espacial $(x,y)$, evoluciona a lo largo del tiempo $t$ y tene crestas en línea recta. El ejemplo prototípico es la función seno o coseno.
Asumamos que una variable $a$ de nuestro sistema fluido geofísico, que puede ser la presión, temperatura, alguna componente de la velocidad, etc. evoluciona de acuerdo a
$$a=A \cos{(k_xx + k_yy - \omega t+ \phi)}.$$El coeficiente $A$ es la amplitud ($-A\le a\le A$), mientras que el argumento
$$\alpha=k_xx + k_yy - \omega t+ \phi$$se conoce como la fase y depende de términos que varían con cada variable independiente y una constante $\phi$ conocida como fase de referencia.
Ls coeficientes $k_x$, $k_y$, $\omega$ de $x$, $y$ y $t$, respectivamente, son el número de onda en $x$, el número de onda en $y$ y la frecuencia angular (aunque solo le decimos frecuencia) e indican la "ondulación" de la onda en $x$ y $y$ y qué tan rápido oscila en el tiempo.
Una expresión equivalente para la onda anterior es:
$$a=A_1 \cos{(k_xx + k_yy - \omega t)} + A_2 \cos{(k_xx + k_yy - \omega t)},$$donde $A1 = A \cos{\phi}$ y $A_2=-A \sin{\phi}$, y
$$a=\cal{R}[A_ce^{i(k_x x+k_y y-\omega t)}],$$donde $\cal{R}[]$ significa "la parte real de" y $A_c=A_1-iA_2 = Ae^{i\phi}$ es un coeficiente de amplitud complejo. ¿Qué forma de expresar a la onda usaremos? Eso dependerá del problema que estemos tratando de resolver.
Veamos un ejemplo de dicha onda:
# Parámetros de la onda
x = np.linspace(-10,10,100)
y = np.linspace(-10,10,100)
t = np.linspace(0,100,60)
X,Y,T = np.meshgrid(x,y,t)
kx = 2
ky = 1
omega = 0.1
phi = np.pi/2
A = 2
Amax= A
a = A*np.cos(kx*X + ky*Y - omega*T + phi)
# grafica usando la función grafica_onda a un tiempo tt
tt = 10
fig, ax, ax_x, ax_y = haz_ejes()
grafica_onda(X[:,:,tt], Y[:,:,tt],a[:,:,tt], tt, ax, ax_x, ax_y)
plt.show()
Variación espacial de la variable $a$
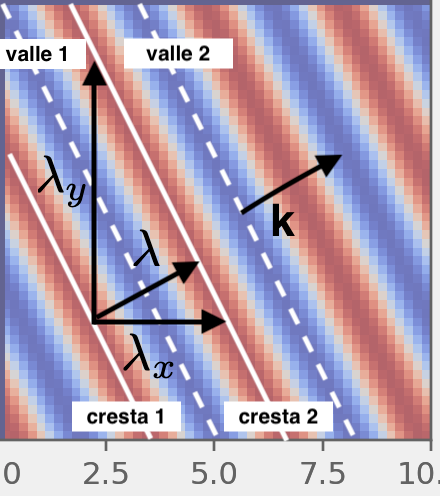
En la gráfica anterior, los valores máximos ($+A$) y mínimos ($-A$) (líneas rojas y azules, respectivamente) de $a$ se conocen como crestas y valles, respectivamente. El valor máximo de $a$ en la cresta corresponde a $+A$ y el minimo a $-A$, el parámetro de amplitud en la ecuación de onda. Las líneas a lo largo de las cuales el valor de $a$ es constante se conocen como líneas de fase.
Examinando la gráfica anterior podemos ver que la estructura de la onda varía más rápido (espacialmente) a lo largo de la dirección x que a lo largo de y.
El valor del número de onda en x $k_x$ es dos veces mayor que el de y $k_y$. Es decir, entre mayor sea el número de onda, más corta será la distancia entre crestas o valles. Esta distancia se conoce como longitud de onda y está relacionada al número de onda como:
$$\lambda_x=\frac{2\pi}{k_x},$$$$\lambda_y=\frac{2\pi}{k_y}.$$¿Qué pasa si modificamos los valores de $k_x$ y $k_y$ de manera que ahora $k_x$=1 y $k_y$=2? ¿o si hacemos $k_x$=1 y $k_y$=0.5?
kx = 1
ky = 2
tt = 10
a = A*np.cos(kx*X + ky*Y - omega*T + phi)
fig, ax, ax_x, ax_y = haz_ejes(figsize=(3,3))
grafica_onda(X[:,:,tt], Y[:,:,tt],a[:,:,tt], tt, ax, ax_x, ax_y)
plt.show()
kx = 1
ky = 0.5
tt = 10
a = A*np.cos(kx*X + ky*Y - omega*T + phi)
fig, ax, ax_x, ax_y = haz_ejes(figsize=(3,3))
grafica_onda(X[:,:,tt], Y[:,:,tt],a[:,:,tt], tt, ax, ax_x, ax_y)
plt.show()
La verdadera longitud de onda es la distancia más corta entre dos crestas: $$\lambda=\frac{2 \pi}{k},$$
donde k es la magnitud del vector número de onda, $\mathbf{k}=(k_x,k_y)=k_x\mathbf{\hat{i}}+k_y\mathbf{\hat{j}}$,
$$k = \sqrt{k_x^2+k_y^2}.$$El vector de onda $\mathbf{k}$ apunta en la dirección perpendicular a las líneas de fase (dirección de ondulación).
Ahora veamos las variaciones temporales de la onda. La siguiente animación nos muestra cómo evoluciona la amplitud de $a(x,y)$ en el tiempo.
# Parámetros de la onda original
kx = 2
ky = 1
a = A*np.cos(kx*X + ky*Y - omega*T + phi)
fig, ax2, ax_x2, ax_y2 = haz_ejes()
anim = FuncAnimation(fig, animate, frames=50, interval=600)
video = anim.to_html5_video()
html = display.HTML(video)
display.display(html)
plt.close()
# omega negativa
omega=-0.1
a = A*np.cos(kx*X + ky*Y - omega*T + phi)
fig, ax2, ax_x2, ax_y2 = haz_ejes(figsize=(3,3))
anim = FuncAnimation(fig, animate, frames=50, interval=600)
video = anim.to_html5_video()
html = display.HTML(video)
display.display(html)
plt.close()
# omega mayor que original (mayor a 0.1)
omega = 1
a = A*np.cos(kx*X + ky*Y - omega*T + phi)
fig, ax2, ax_x2, ax_y2 = haz_ejes(figsize=(3,3))
anim = FuncAnimation(fig, animate, frames=50, interval=600)
video = anim.to_html5_video()
html = display.HTML(video)
display.display(html)
plt.close()
# omega menor que original (menor a 0.1)
omega=0.01
a = A*np.cos(kx*X + ky*Y - omega*T + phi)
fig, ax2, ax_x2, ax_y2 = haz_ejes(figsize=(3,3))
anim = FuncAnimation(fig, animate, frames=50, interval=600)
video = anim.to_html5_video()
html = display.HTML(video)
display.display(html)
plt.close()
Si nos paramos en un punto $(x,y)$, veremos una señal oscilatoria. El intervalo de tiempo entre nuestra observación de una cresta y otra (o cualquier fase constante que elijamos) es el requerido para que la porción $\omega t$ de la fase aumente en $2\pi$, es decir, "de una vuleta". Este tiempo es el periodo de la onda:
$$T=\frac{2 \pi}{\omega}.$$Ahora sigamos la progresión de una cresta en particular de un tiempo $t_1$ a un tiempo $t_2$, es decir, a lo largo de un intervalo de tiempo $t_2$-$t_1$. La intersección de la cresta con el eje $x$ se ha avanzado una distancia $\Delta x=\omega t_2/k_x-\omega t_1/k_x=\omega \Delta t/k_x$. Esto define la velocidad de propagación de la onda a lo largo de la dirección x: $$c_x=\frac{\Delta x}{\Delta t}=\frac{\omega}{k_x}.$$
Similarmente, para la dirección y:
$$c_y=\frac{\Delta y}{\Delta t}=\frac{\omega}{k_y}.$$La verdadera velocidad de propagacion de la señal está dada por la distancia $\Delta s$ que recorre una línea de fase en el intervalo de tiempo $\Delta t$:
$$\Delta s = \frac{\omega \Delta t}{k},$$lo que nos da una velocidad de propagación
$$c=\frac{\delta s}{\Delta t}=\frac{\omega}{k}.$$Toda las líneas de fase se mueven a la misma velocidad, por lo que $c$ se conoce como velocidad de fase y depende de ambas, frecuencia y número de onda.
Nota que como $c^2 \neq c_x^2+c_y^2$, el par $c_x$, $c_y$ no forma un vector físicamente (del mismo modo que $\lambda_x$, $\lambda_y$ no forman un vector).
Usualmente, $\omega$ solo es función de $k_x$ y $k_y$. Como $\omega$ es función del número de onda, la velocidad también lo será:
$$c=\frac{\omega(k_x,k_y)}{\sqrt{k_x^2+k_y^2}}=c(k_x,k_y)$$.
Físicamente, esto significa que las ondas que componen a una señal viajarán a distinta velocidad (cada una tiene un número de onda característico) y habrá una distorsión de la estructura original de la onda conforme avance el tiempo. ste fenómeno se conoce como dispersión y la función matemática que relaciona a $\omega$ y $k$ se concoe como relación de dispersión.
La relación de dispersión se puede representar en dos dimensiones, como el conjunto de curvas en el plano $(k_x,k_y)$ tales que $\omega$ es constante. Aquí va un ejemplo para la relación de dispersión dada por:
$$\omega=\frac{2k_x}{(k_x^2+k_y^2+1)}.$$# relación de dispersión
kx_vec = np.linspace(-10,10,50)
ky_vec = np.linspace(-10,10,50)
KX,KY = np.meshgrid(kx_vec,ky_vec)
omega_vec = 2*KX / (KX**2+KY**2+np.ones_like(KY))
fig, ax = plt.subplots(1,1,figsize=(5,6))
cn = ax.contour(KX,KY,omega_vec,10)
ax.clabel(cn, fmt='%1.1f')
ax.set_xlim(0,10)
ax.set_ylim(-6,6)
ax.set_xlabel('$k_x$')
ax.set_ylabel('$k_y$')
ax.set_title(r'relación de dispersión $\omega(k_x,k_y)$')
ax.set_aspect(1)
ax.grid()
plt.show()
En algunos casos físicos particulares ocurre que la relación de dispersión es solo una constante de proporcionalidad entre $\omega$ y $k$, en cuyo caso la velocidad de fase es la misma para todos los números de onda y la señal mantiene su estructura y forma en el tiempo. En este caso decimos que la onda es no dispersiva.
Veamos un ejemplo de onda dispersiva y uno de una onda no dispersiva:
# Onda no dispersiva, suma de dos ondas con la misma velocidad de fase c=0.045
kx1 = 2
ky1 = 1
kx2 = 4
ky2 = 2
omega1 = 0.1
omega2 = 0.2
phi = np.pi/2
A1 = 2
A2 = 2
Amax= A1+A2
a = A1*np.cos(kx1*X + ky1*Y - omega1*T + phi)+A2*np.cos(kx2*X + ky2*Y - omega2*T + phi)
fig, ax2, ax_x2, ax_y2 = haz_ejes(figsize=(4,4))
anim = FuncAnimation(fig, animate, frames=50, interval=600)
video = anim.to_html5_video()
html = display.HTML(video)
display.display(html)
plt.close()
# Onda dispersiva, suma de dos ondas con distinta velocidad de
# fase c1=0.045 m/s, c2=0.13 m/s
kx1 = 2
ky1 = 1
kx2 = 4
ky2 = 2
omega1 = 0.1
omega2 = 0.57
phi = np.pi/2
A1 = 2
A2 = 2
Amax= A1+A2
a = A1*np.cos(kx1*X + ky1*Y - omega1*T + phi)+A2*np.cos(kx2*X + ky2*Y - omega2*T + phi)
fig, ax2, ax_x2, ax_y2 = haz_ejes(figsize=(5,4))
anim = FuncAnimation(fig, animate, frames=50, interval=600)
video = anim.to_html5_video()
html = display.HTML(video)
display.display(html)
plt.close()
Una onda o señal está constituida, en general, de varias ondas o señales "puras". La superposición de estas ondas genera interferencia contructiva o destructiva. En las zonas en las que hay interferencia constructiva, la amplitud de la onda total es mayor; en zonas de intereferencia destructiva la amplitud d ela onda total es menor. Así, la distribución de la energía es función del grupo de ondas que constutuyen a la onda total (una onda simple tiene una distibución de energía uniforme).
La distribución de energía del grupo de ondas depende, justamente, de cómo varían o cómo se mueven las zonas de interefencia constructiva y destructiva.
Para ilustrar esto consideremos dos ondas con la misma amplitud $A$ y números de onda similares
$$a = A \cos{(k_1x-\omega_1 t)}+A \cos{(k_2x-\omega_2 t)},$$donde los valores de $k_1$ y $k_2$ están cercanos al valor de su promedio $(k_1+k_2)/2$ y la diferencia $\Delta k =k_1-k_2$ es mucho menor que las $|k's|$. Como ambas ondas obedecen la dispersión de onda $\omega(k)$ del sistema dinámico (dado por a suma de ambas), las dos frecuencias están cerca del valor promedio y su diferencia es mucho mayor que este valor.
Con un poco de trigonometría podemos transformar la ecuación original para $a$ en
$$a=2A(\cos{\frac{\Delta k}{2}x-\frac{\Delta \omega}{2}t})\cos{(kx-\omega t)},$$que es el producto de dos ondas: el segundo seno corresponde a una onda "promedio" y la primera corresponde a una onda de frecuencia y número de onda mucho más pequeños que los originales. El efecto de esto es que la onda con $(k,\omega)$ (onda de longitud mucho más corta) parece modulada por la onda larga y su amplitud, dada por $2A(\cos{(\Delta kx-\Delta \omega t)/2})$, varía lentamente en el tiempo y en el espacio:
A = 2
Amax=6
k1 = 1.9
k2 = 2.1
k = (k2+k1)/2
omega1 = 2.1
omega2 = 1.9
omega = (omega1+omega2)/2
x = np.linspace(0,100,400)
t = np.linspace(0,10*np.pi,100)
X,T = np.meshgrid(x,t)
a = A*np.cos(k1*X-omega1*T)+A*np.cos(k2*X-omega2*T)
def grafica_grupo(ax,a,x,t,A=2):
ax.plot(x,a)
ax.set_title('t=%1.1f s' %t)
ax.set_xlabel('x')
ax.set_ylabel('a')
ax.set_xlim(np.min(x), np.max(x))
ax.set_ylim(-A, A)
def anima_grupo(tt):
ax.clear()
grafica_grupo(ax,a[tt,:],x,t[tt],A=Amax)
fig, ax = plt.subplots(1,1,figsize=(5,3.5))
anim = FuncAnimation(fig, anima_grupo, frames=50, interval=100)
video = anim.to_html5_video()
html = display.HTML(video)
display.display(html)
plt.close()
La señal envolvente tiene una longitud de onda ($\lambda'=2\pi/\Delta k$) mucho mayor que la señal total ($\lambda=2\pi/k$).
La onda se propaga a velocidad $c=\omega/k$ mientras que el paquete o envolvente se propaga a velocidad $c'=\Delta \omega/\Delta k$.
Para una diferencia infinitesimal en número de onda, la velocidad de la envolvente o el grupo está dada por:
$$c_g=\frac{d\omega}{dk}.$$La velocidad de grupo representa la velocidad a la que las ondas transportan energía.
Esto se puede extender a ondas en más de una dimensión:
$$c_gx=\frac{\partial\omega}{\partial k_x}, c_gy=\frac{\partial\omega}{\partial k_y}, ...$$Dado que estas expresiones son las componentes del gradiente de la función de onda $\omega(k_x,k_y)$, se pueden interpretar como las componentes de un vector físico asociado a la velocidad de grupo:
$$\mathbf{c_g}=\nabla_k\omega.$$Este vector apunta perpendicularmente a las curvas $\omega$ (de la gráfica de la curva de dispersión de arriba) hacia la dirección en la que crece $\omega$.
Alineando los ejes $k_x$ y $k_y$ con los ejes $x$ y $y$ del plano nos da la dirección de propagación de la energía en el espacio.