Ejemplo de una solución numérica¶
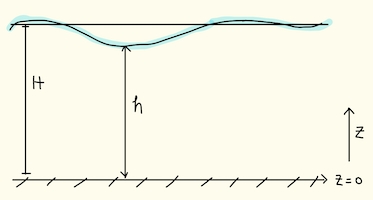
En este notebook vamos a resolver las ecuaciones de aguas someras linealizadas para un dominio rectangular. Esto quiere decir que encontraremos la altura de la superficie libre del mar, $h=h(x,y,t)$, y las componentes horizontales de velocidad $\vec{u}(x,y,t)=(u,v)$ a un tiempo dado integrando numéricamente el siguiente sistema de ecuaciones:
$$\frac{\partial{u}}{\partial{t}}=g\frac{\partial{h}}{\partial{x}}$$$$\frac{\partial{v}}{\partial{t}}=g\frac{\partial{h}}{\partial{y}}$$$$\frac{\partial{h}}{\partial{t}}+H\left(\frac{\partial{u}}{\partial{x}}+\frac{\partial{v}}{\partial{y}}\right)=0,$$en donde $H$ es la profundidad de la capa sin perturbar y $g$ la aceleración de la gravedad.
Además, practicaremos la separación de código en funciones para generar nuestro primer modelo numérico.
# Importamos las bibliotecas y paquetes de python que usaremos para correr este notebook
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# Definición de constantes
g = 9.81 # gravedad en m/s2
rho = 1025 # densidad del agua de mar en km/m3
X = 200 # número de puntos de la malla en X
Y = 300 # número de puntos de la malla en Y
Xvec = np.arange(0,X,1) # vector con puntos de la malla (de 0 a X)
Yvec = np.arange(0,Y,1) # vector con puntos de la malla (de 0 a Y)
# Batimetría
H = np.ones((X,Y))*1000 # Arreglo de dimensiones (X,Y) lleno del valor 1000, o un fondo plano de 1000 m de profundidad
# Inicialización de las variables
h = H*0 # Anomalía de la profundidad
h0 = h # Anomalía de la profundidad en tiempo t=0
h2 = h # Anomalía de la profundidad en tiempo t=2
u0 = np.zeros((X+1,Y)) # Velocidad inicial (en tiempo t=0)
u2 = u0 # Velocidad en tiempo t=2
v0 = np.zeros((X,Y+1)) # Velocidad en tiempo t=0
v2 = v0 # Velocidad en tiempo t=2
DelX = 100 # Resolución espacial en m
DelT = 0.5 # Paso de tiempo en segundos
CFL = np.sqrt(g*np.max(H))*DelT/DelX # Condición de estabilidad Courant-Friederich-Levy
Una vez que definimos el dominio espacial en donde resolveremos las ecuaciones, generemos una perturbación en la superficie libre de la forma
$$h(x,y)= B \exp\left(-\frac{x^2}{2\sigma_x^2}-\frac{y^2}{2\sigma_y^2}\right),$$donde B nos dará la altura inicial de la perturbación y $\sigma_x$, $\sigma_y$ la desviación estándar o el "ancho" de la gausiana en las direcciones $x$ y $y$, respectivamente.
# Perturbación inicial de la superficie (un tope gaussiano)
z = np.zeros((X,Y))
x,y = np.meshgrid(Xvec,Yvec) # ¿Sabes qué hace la función meshgrid? Trata help(np.meshgrid) o consulta
# https://numpy.org/doc/stable/reference/generated/numpy.meshgrid.html
#help(np.meshgrid)
print(np.shape(x), np.shape(y))
sigma_x = 0.2*X/4
sigma_y = 0.2*X/4
B = 1 # Altura inicial de la perturbación
z = B * np.exp(-((x-100)**2/(2*sigma_x**2) + (y-150)**2/(2*sigma_y**2)))
print(np.max(z))
# Gráfica rápida
plt.pcolormesh(z)
plt.colorbar()
plt.show()
O podemos hacer una gráfica más ilustrativa de la perturbación inicial. Para eso necesitaremos importar la biblioteca mplot3d:
from mpl_toolkits import mplot3d
fig = plt.figure(figsize=(8,5))
ax = plt.axes(projection='3d')
surf = ax.plot_surface(x, y, z,cmap='viridis', edgecolor='none',antialiased=False)
ax.set_title('Perturbación inicial')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
fig.colorbar(surf, shrink=0.5, aspect=5, label='m')
plt.show()
Ahora sí, resolvamos el sistema de ecuaciones con condiciones iniciales y de frontera:
# timestepping
nt = 200
for t in range(1,nt):
if t==1:
h0 = np.transpose(z)
# Velocidad 0 en las fronteras
u0[-1,:] = 0
u0[0,:] = 0
v0[:,0] = 0
v0[:,-1] = 0
u2[1:X,0:Y] = u0[1:X,0:Y] - g*(h0[1:X,0:Y] - h0[0:X-1,0:Y]) * DelT/DelX
v2[0:X,1:Y] = v0[0:X,1:Y] - g*(h0[0:X,1:Y] - h0[0:X,0:Y-1]) * DelT/DelX
h2[0:X,0:Y] = (h0[0:X,0:Y] - H[0:X,0:Y]*
(u2[1:X+1,0:Y] - u2[0:X,0:Y] +
v2[0:X,1:Y+1] - v2[0:X,0:Y])* DelT/DelX)
u0 = u2
v0 = v2
h0 = h2
if t%10 == 0:
fig = plt.figure(figsize=(8,5))
ax = plt.axes(projection='3d')
surf = ax.plot_surface(x, y, np.transpose(h2), cmap='viridis',
edgecolor='none',antialiased=False)
ax.set_title('Superfice libre después de %1.1f s' %t)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_zlim(-0.75,0.75)
fig.colorbar(surf, shrink=0.5, aspect=5, label='m')
plt.show()
Hagamos un pequeño modelo¶
Ahora que hemos desarrollado código para resolver este sistema de ecuaciones sería práctico agruparlo en unidades de código que hacen una sola tarea, es decir, en funciones. Así podremos correr nuestro modelo con distintos parámetros sin tener que copiar y pegar todo el código que escibimos arriba.
Para ello definiremos 5 funciones:
inicia será la función que inicialice las variables del modelo;
perturba generará las condiciones inciales en la superfice libre;
adelanta será la función que integra las ecuaciones discretizadas en el tiempo,
grafica generará la gráfica de la superficie libre y
corre será la función maestra que llama a las demás funciones ("wrapper").
def inicializa(X,Y,g,Hmax,DelT,DelX,rho):
'''Esta función inicializa la malla, variables dinámicas y constantes para usar en el modelo.
OUTPUT
X, Y, x, y, g, Hmax, DelT, DelX, rho
'''
Xvec = np.arange(0,X,1)
Yvec = np.arange(0,Y,1)
x,y = np.meshgrid(Xvec,Yvec)
# Batimetría
H = np.ones((X,Y))*Hmax # Arreglo de dimensiones (X,Y) lleno del valor 1000
# Inicialización de las variables dinámicas
h = H*0 # Anomalía de la profundidad
h0 = h # Anomalía de la profundidad en tiempo t=0
h2 = h # Anomalía de la profundidad en tiempo t=2
u0 = np.zeros((X+1,Y)) # Velocidad inicial (en tiempo t=0)
u2 = u0 # Velocidad en tiempo t=2
v0 = np.zeros((X,Y+1)) # Velocidad en tiempo t=0
v2 = v0 # Velocidad en tiempo t=2
CFL = np.sqrt(g*np.max(H))*DelT/DelX # Condición de estabilidad Courant-Friederich-Levy
print('la malla es de dimensiones:')
print(np.shape(x))
print('El paso de tiempo es %1.2f' %DelT)
print('La resolución espacial es %1.2f' %DelX)
print('El valor de CFL es %f' %CFL)
return(X, Y, x, y, h0, h2, u0, u2, v0, v2, H, g, Hmax, DelT, DelX, rho)
def perturba(x, y, X, Y, B, s_x, s_y):
'''Esta función genera una perturbación inicial gausiana en la superficie libre.
INPUT
x, y :: arreglos numpy 2D de dim (X,Y), la malla
B :: real, Altura inicial de la perturbación
s_x :: factor para calcular la desviación estándar de la gausiana en dirección x
como s_x*X/4
s_y :: factor para calcular la desviación estándar de la gausiana en dirección x
como s_y*X/4
OUTPUT
z :: arreglo numpy 2D dim (X,Y) con la gausiana.
'''
sigma_x = s_x*X/4
sigma_y = s_y*X/4
z = B * np.exp(-((x-int(X/2))**2/(2*sigma_x**2) + (y-int(Y/2))**2/(2*sigma_y**2)))
return(z)
def adelanta(u0, u2, v0, v2, h0, h2, H, g, delT, delX):
'''Esta función evoluciona las componentes de velocidad (u0, v0, u2, v2)
y la superficie libre (h0, h2) en un paso de tiempo de tamaño delT, para
una malla regular de resolución delX.
INPUT
u0 :: arreglo numpy 2D, componente x de la velocidad en nt-1, dim(X+1,Y)
u2 :: arreglo numpy 2D, componente x de la velocidad en nt+1, dim(X+1,Y)
v0 :: arreglo numpy 2D, componente y de la velocidad en nt-1, dim(X,Y+1)
v2 :: arreglo numpy 2D, componente y de la velocidad en nt+1, dim(X,Y+1)
h0 :: arreglo numpy 2D, superificie libre en nt-1, dim(X,Y)
h2 :: arreglo numpy 2D, superificie libre en nt+1, dim(X,Y)
H :: arreglo numpy 2D, profundidad, dim(X,Y)
g :: escalar, valor de la gravedad en m/s2
delT :: escalar, paso de tiempo en segundos
delX :: escalar, resolución espacial en kilometros
OUTPUT
u0 :: arreglo numpy 2D, componente x de la velocidad en nt-1, dim(X+1,Y)
u2 :: arreglo numpy 2D, componente x de la velocidad en nt+1, dim(X+1,Y)
v0 :: arreglo numpy 2D, componente y de la velocidad en nt-1, dim(X,Y+1)
v2 :: arreglo numpy 2D, componente y de la velocidad en nt+1, dim(X,Y+1)
h0 :: arreglo numpy 2D, superificie libre en nt-1, dim(X,Y)
h2 :: arreglo numpy 2D, superificie libre en nt+1, dim(X,Y)
'''
# Condiciones de frontera
u0[-1,:] = 0
u0[0,:] = 0
v0[:,0] = 0
v0[:,-1] = 0
# Evolución temporal
u2[1:X,0:Y] = u0[1:X,0:Y] - g*(h0[1:X,0:Y] - h0[0:X-1,0:Y]) * DelT/DelX
v2[0:X,1:Y] = v0[0:X,1:Y] - g*(h0[0:X,1:Y] - h0[0:X,0:Y-1]) * DelT/DelX
h2[0:X,0:Y] = (h0[0:X,0:Y] - H[0:X,0:Y]*
(u2[1:X+1,0:Y] - u2[0:X,0:Y] +
v2[0:X,1:Y+1] - v2[0:X,0:Y])* DelT/DelX)
# Actualiza arreglos
u0 = u2
v0 = v2
h0 = h2
return(u0, u2, v0, v2, h0, h2)
def grafica(t, x, y, h2):
'''Esta función genera una gráfica de la superficie libre'''
fig = plt.figure(figsize=(8,5))
ax = plt.axes(projection='3d')
surf = ax.plot_surface(x, y, np.transpose(h2), cmap='viridis',
edgecolor='none',antialiased=False)
ax.set_title('Superfice libre después de %1.1f s' %t)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_zlim(-0.75,0.75)
fig.colorbar(surf, shrink=0.5, aspect=5, label='m')
plt.show()
return(ax)
def corre(nt=200, X=200, Y=300, g=9.81, Hmax=1000, DelT = 0.5, DelX=100, rho = 1025,
B=1, s_x=0.2, s_y=0.2):
'''Esta función corre el modelo con los siguente valores default:
nt = 200, número de pasos de tempo.
X = 200, número de puntos de la malla en X y longitud máxima en X
Y = 300, número de puntos de la malla en Y y longitud máxima en Y
g = 9.81, gravedad en m/s2
Hmax = 1000, valor de la profunidad máxima en m
DelT = 0.5, paso de tiempo
DelX = 100, resolución espacial de la malla
rho = 1025, densidad del agua de mar en km/m
B :: real, Altura inicial de la perturbación, default es 1 m
s_x :: factor para calcular la desviación estándar de la gausiana en dirección x
como s_x*X/4, default es 0.2
s_y :: factor para calcular la desviación estándar de la gausiana en dirección x
como s_y*X/4, default es 0.2 '''
# Inicializa
X, Y, x, y, h0, h2, u0, u2, v0, v2, H, g, Hmax, DelT, DelX, rho = inicializa(X,Y,g,Hmax,DelT,DelX,rho)
# Genera pa perturbación gausiana
z = perturba(x, y, X, Y, B, s_x, s_y)
# integra en el tiempo y grafica
for t in range(nt):
if t==0:
h0 = np.transpose(z)
u0, u2, v0, v2, h0, h2 = adelanta(u0, u2, v0, v2, h0, h2, H, g, DelT, DelX)
if t%10 == 0:
grafica(t, x, y, h2)
Así podemos llamar al modelo de manera limpia y rápida:
corre()
Y rápidamente podemos cambiar los parámetros de la corrida. Por ejemplo, hagamos una gausiana más ancha a lo largo de x cambiando el valor de s_x a 0.4:
corre(s_x=0.4)
Ejercicio:¶
Genera tu propia corrida cambiando los parámetros del modelo. Por ejemplo, integra por más pasos de tiempo, cambia la perturbación inicial y comenta cómo cambia la solución respecto a la configuración default.
Intenta al menos 2 configuraciones distintas y escribe una justificación de por qué intentaste cambiar los parámetros que cambiaste, qué esperabas obtener y qué obtuviste.
Animación¶
Es útil tener las gráficas de la salida de nuestro modelo para compartir nuestros resultados y comparar la evolución del sistema en distintos momentos, pero también sería útil visualizar esta evolución temporal. Para eso podemos usar el módulo animation de matplotlib y explorar rápidamente el efecto de los distintos parámetros del modelo.
Hay algunos parámetros que debemos definir:
import matplotlib.animation
from IPython.display import HTML
matplotlib.rcParams['animation.embed_limit'] = 2**128 # para animaciones dentro del notebook de mas de 2Mb
plt.rcParams["animation.html"] = "jshtml"
plt.rcParams['figure.dpi'] = 150
plt.ioff()
Ahora construiremos la animación usando las funciones que definimos anteriormente para nuestro modelo, pero no utilizaremos la función wrapper corre ni la función grafica. Las acciones de estas dos funciones estarán dentro la función anima. La función matplotlib.animate utiliza a esta función para cada cuadro de la animación, es decir, actualiza la animación para cada cuadro llamando a anima.
Antes de animar debemos construir la figura y los ejes que serán la base de la animación. Después definimos los parámetros del modelo, inicializamos las variables y generamos la perturbación inicial.
Posteriormente viene la definición de la función anima, en donde adelantamos el sistema en un paso de tiempo (en este caso cada paso de tiempo será un cuadro del video) y grafica el estado del sistema. Esta definición puede ir en otro lado, claro.
Finalmente llamamos a matplotlib.animate para que genere la animación. Este paso puede tardar algunos minutos dependiendo de cuántos cuadros hayas seleccionado (el valor nt). animation.FuncAnimation toma como argumentos la figura inicial, la función para adelantar el cuadro, los argumentos de esa función (los que no son el número de cuadro) y el número de cuadros. Hay otros argumentos que puedes consultar en la documentación.
fig = plt.figure(figsize=(8,5))
ax = plt.axes(projection='3d')
nt = 10 # Más de 50 pasos puede ser tardado dependiendo de tu computadora,
# intenta un número pequeño para probar, por ejemplo 10.
X = 200
Y = 300
g = 9.81
Hmax = 1000
DelT = 0.5
DelX = 100
rho = 1025
B = 1
s_x = 0.2
s_y = 0.2
# Inicializa
X, Y, x, y, h0, h2, u0, u2, v0, v2, H, g, Hmax, DelT, DelX, rho = inicializa(X,Y,g,Hmax,DelT,DelX,rho)
# Genera una perturbación gausiana
z = perturba(x, y, X, Y, B, s_x, s_y)
def animate(t, x, y, u0, u2, v0, v2, h0, h2, H, g, DelT, DelX ):
plt.cla()
if t==0:
h0 = np.transpose(z)
u0, u2, v0, v2, h0, h2 = adelanta(u0, u2, v0, v2, h0, h2, H, g, DelT, DelX)
# graficar
surf = ax.plot_surface(x, y, np.transpose(h2), cmap='viridis',
edgecolor='none',antialiased=False)
ax.set_title('Superfice libre después de %1.1f s' %t)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_zlim(-0.75,0.75)
anim = matplotlib.animation.FuncAnimation(fig,
animate,
fargs=(x, y, u0, u2, v0, v2, h0, h2, H, g, DelT, DelX),
frames=nt)
anim
Ejercicio:¶
Explora los parámetros del modelo como hiciste en el ejercicio anterior pero usando animaciones.
Salvar animaciones¶
Si quieren ir más allá de ver animaciones en su notebook pueden salvar su animación como gif animado o video mp4. Para ello es probable que deban instalar software extra y por eso lo dejamos como actividad opcional. Pueden seguir este post que los llevará de la mano para salvar en cualquiera de los dos formatos.